黎雪健,李雪年,李建樑
(长沙理工大学 数学与统计学院,湖南 长沙 410114)
本文研究的是可穿透无穷曲面的时谐声波反散射问题.对于可穿透无穷曲面,声波可以穿透到曲面以下进行传播.实际生活中,像海平面、地面等都是可穿透无穷曲面,这类问题在诸如海洋声呐、地下管道无损探测、雷达技术等众多领域有着广泛的应用,因此对可穿透无穷曲面散射问题的研究有着重要的科学意义.一般而言,可穿透无穷曲面的时谐声波散射问题由两部分组成.第一部分是正散射问题,即给定入射场和无穷曲面,理论上证明散射场的适定性,也就是散射场是否存在唯一且连续依赖于入射场;
数值上发展快速且稳定的数值算法求解散射场.对于无穷曲面正散射问题的理论研究,主要包括两类方法:变分法[1]和边界积分方程方法[2-5].在这两类方法的基础上建立了相应的数值算法,例如:基于变分法的完美匹配层(PML)方法[6]和基于边界积分方程的Nystrm方法[7-8]等.
理论上,文献[1]运用变分法研究了基于声软型无穷曲面且带有紧支集源项的时谐声波正散射问题.运用边界积分方程方法来研究无穷曲面散射问题时,针对无穷曲面是平面的局部扰动且为声软或声硬的情形,利用反射原理可以把无穷曲面散射问题归结于有界区域上的第二类积分方程问题,文献[9-10]中应用经典Fredholm理论证明了积分方程解的适定性.当无穷曲面是平面的全局扰动时,由于散射曲面的无界性,导致相关的积分算子不再具有紧性,从而经典Fredholm理论不再适用.文献[11-12]建立了适用于此情形的广义Fredholm理论,从而为积分方程方法解决全局扰动的无穷曲面散射问题提供了强有力的数学工具.针对声软型和阻尼型全局扰动曲面的正散射问题,文献[5]运用广义Fredholm理论证明了此类问题解的适定性.更多运用广义Fredholm理论证明散射问题解的适定性的相关研究可以参见文献[3,13-14].文献[14]中考虑了一个特殊的二维传输问题,要求可穿透曲面以下是吸收介质,在曲面上满足传输条件,在曲面上下区域分别满足不同波数的Helmholtz方程,对于这个问题,文献[14]证明了解的适定性.
数值上,Meier等[15]给出了一类适用于粗糙无穷曲面散射问题的Nystrm方法,并建立了该方法的稳定性和收敛性,证明了其收敛速度取决于无穷曲面的光滑性.利用文献[15]中的结果,文献[7,16]分别建立了针对不可穿透的无穷曲面以及可穿透无穷曲面正散射问题的Nystrm方法.
第二部分是反散射问题,即通过测量远场或近场的散射数据来重构无穷曲面的位置和形状.众所周知,反散射问题是高度非线性而且不适定,即测量数据中的一个小扰动会给无穷曲面的重构带来巨大的误差,这给反问题的研究带来了很大的困难.理论上反散射问题主要研究唯一性[3,12],即需要多少入射场产生的散射数据能够唯一确定无穷曲面;
数值上反散射问题主要研究数值重构方法.文中主要考虑的是反问题的数值重构方法,这也是实际应用中最为关心的问题.目前,反散射问题的数值重构方法主要有两类,第一类是迭代方法,包括牛顿迭代法[17]、非线性积分方程方法[7-8,18]、Kirsch-Kress方法[23]等;
第二类是非迭代方法,包括奇异源方法[20]、 线性采样方法[21]、点源方法[22]、分解方法[23]等.
对于牛顿迭代法,通常需要计算近场或远场关于无穷曲面的Fréchet导数,这个导数是通过相关的边值问题[24]给出.为了减少计算量,Kress等[18]针对有界障碍反散射问题提出了一种新的迭代方法,称为非线性积分方程方法,这个方法采用积分算子的显式表达近似Fréchet导数.非线性积分方程方法的主要思想是建立反散射问题和一个积分系统的等价性,从而通过求解积分系统来求解反散射问题.与其他迭代方法相比较,非线性积分方程方法的主要优点在于其计算量更小,如果选取恰当的初始值,往往能得到比较好的重构结果.因此近年来,非线性积分方程方法在求解反散射问题的研究中得到了广泛的应用,例如:有界障碍反散射问题[25-26]、有夹杂物和裂纹的反散射问题[27]、无穷曲面反散射问题[7-8]等.
文献[7-8]将非线性积分方程方法推广到不可穿透的无穷曲面,分别重构了声软型和阻尼型无穷曲面.但是目前对于可穿透无穷曲面的情形暂时没有相关研究.由于散射曲面的无界性和可穿透性,使得该反散射问题的研究更具有挑战性.本文主要考虑将非线性积分方程方法推广到可穿透无穷曲面反散射问题中,利用散射场和透射场的积分表示可以得到散射场和透射场关于无穷曲面的近似Fréchet导数,基于此Fréchet导数以及无穷曲面上下方近场的测量数据,发展了该问题的非线性积分方程方法.由于Fréchet导数是一个近似的结果,为了得到更精确的重构,文中使用多频近场数据,首先给定一个初始猜测,根据低频数据得到无穷曲面的大致形状,然后将低频数据的重构结果作为高频数据的初始猜测,最后得到无穷曲面的精确重构.数值算例表明,该问题的非线性积分方程方法是一种精确且稳定的数值重构方法.
本节将给出可穿透无穷曲面散射问题的数学模型.如图1所示,假设在二维空间R2中存在一个可穿透无穷界面Γ:
Γ=Γf:={x=(x1,x2)∈R2|x2=f(x1)},
式中:f∈B,这里B是一个函数空间,其定义如下:对于两个正数c1,c2,
B=B(c1,c2)={f∈C2(R)|f(s)≥c1,s∈R,‖f‖C2(R)≤c2},

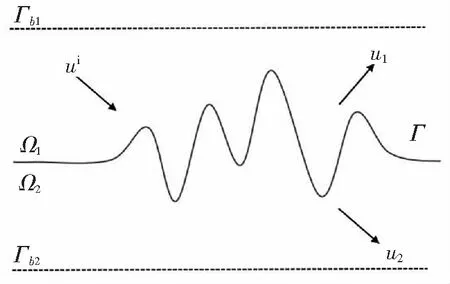
图1 散射问题的几何表示Fig.1 Geometry of the scattering problem
该无穷界面Γf把二维空间R2分成上下两个区域,分别记为Ω1和Ω2:
假设k1和k2分别是上下两个区域Ω1和Ω2对应的波数.选用入射场ui(x)为多个点源叠加的形式,即
(1)
当给定形式(1)的入射场从界面上方入射时,会在Ω1中产生散射场u1,在Ω2中产生透射场u2,其中u1和u2分别在Ω1和Ω2中满足如下对应波数的Helmholtz方程:
(2)
(3)
总场在Ω1中表现为入射场和散射场的叠加ui+u1,在Ω2中表现为透射场u2.在界面Γ上u1和u2满足传输边界条件,
u1-u2=-ui,
(4)
(5)
除此之外,为了保证散射波是向上传输的以及透射波是向下传输的,u1和u2需要分别满足向上传输散射条件(UPRC)和向下传输散射条件(DPRC)[3].
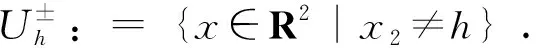
(6)

(7)
另外要求散射场u1和透射场u2在x2方向满足一定的增长性条件:对任意β∈R,
因此,可以把散射问题归结为以下形式:
(8)
式中,ν是指向Ω1的外法向.由文献[14]的结果可知式(8)是适定的,文献[16]基于边界积分方程方法求解了式(8)的数值解.
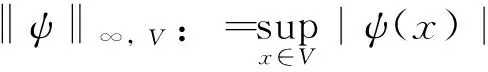
由文献[16]的结果可知,对于一个固定的无穷粗糙界面Γ,可以用单层位势和双层位势的耦合来表示式(8)的解,形式如下:
(9)

(10)
式中:
对于x∈Γ,定义边界积分算子:
根据单层位势和双层位势的跳跃关系(参见文献[5]的附录A)以及文献[14]中的引理(4.1~4.3)和传输条件,可以将式(8)简化为以下Γ上的边界积分方程:
MIφ=g,
(11)
式中:
由文献[14]的结果可知,边界积分方程(11)存在唯一解.对∀f∈B,如果φ是边界积分方程(11)的唯一解,则由式(9)给出的u1,u2是原散射问题式(8)的唯一解,进一步u1,u2连续依赖于‖g1‖∞,Γ,‖g2‖∞,Γ以及∇u1,∇u2连续依赖于‖g1‖1,α,Γ,‖g2‖0,α,Γ,从而可以得到原散射问题的存在性,原散射问题的唯一性直接可由文献[12]的结果得到.
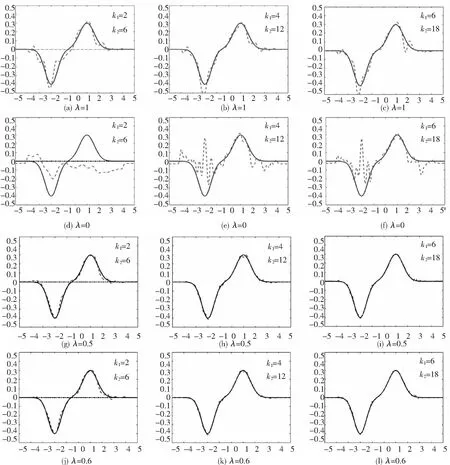
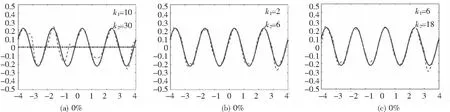
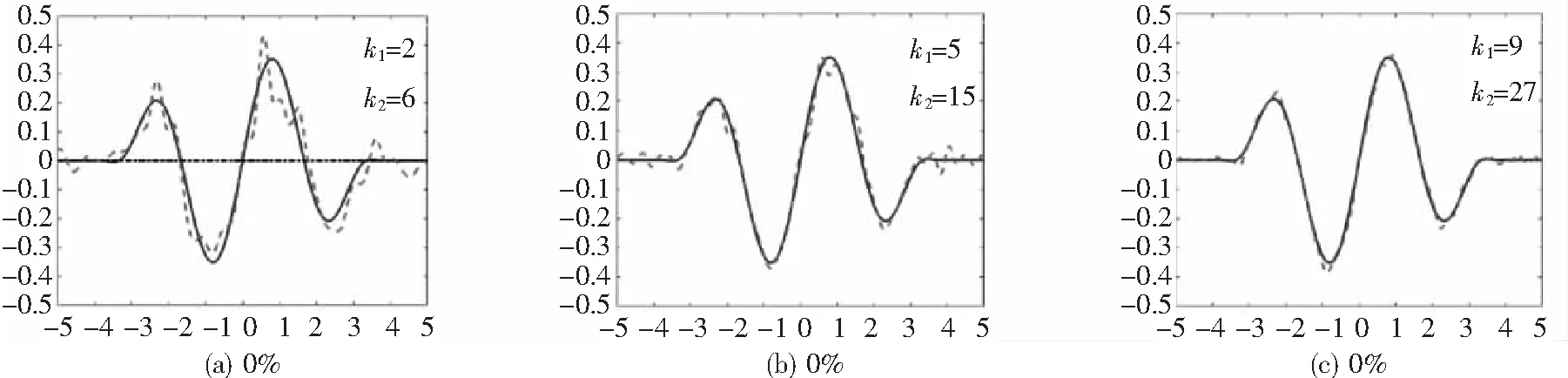
在这一部分考虑的反散射问题是:给定入射场ui(x),根据测量的近场数据ub1(x):=u1(x)|Γb1,A,ub2(x):=u2(x)|Γb2,A,重构未知界面Γ的位置和形状.其中,接收平面Γbi,A:={x∈R2:x2=bi,|x1|≤A},i=1,2,这里b1>f+,b2 首先推导积分系统,利用Nyström方法求解边界积分方程(11)可得到密度函数φ1,φ2,详细步骤可参考文献[19].这样散射场u1和透射场u2在接收平面Γb1,Γb2上的值就可以表示为 (12) 因此,可以得到积分系统式(11)和式(12)和原反散射问题的等价性. 定理2.1如果无穷界面Γf可以被近场u1(x)|Γb1,u2(x)|Γb2唯一确定.则对于给定的近场ub1(x):=u1(x)|Γb1,ub2(x):=u2(x)|Γb2,界面Γf是反散射问题的解当且仅当(Γf,φ1,φ2)是积分系统式(11)和式(12)的解. 证明如果(Γf,φ1,φ2)是积分系统式(11)和式(12)的解,定义: 反过来,给定近场ub1(x),ub2(x),假设Γf是反散射问题的解,那么问题式(8)的解为 式中:φ1,φ2满足式(11).根据问题式(8)的唯一性,可知式(12)成立,从而(Γf,φ1,φ2)是积分系统式(11)和式(12)的解.证明结束. 于是就把散射场u1和透射场u2重写为以下形式: (13) 对于x∈Γ,重新定义边界积分算子: 因此,可以将问题式(8)简化为以下Γ上的边界积分方程: Mφ=g. (14) 式中: 将散射场u1和透射场u2在接收平面Γb1,Γb2上的值重新表示为 (15) 于是可以得到新的积分系统式(13)和式(14),根据等价性定理,可以通过求解新的积分系统式(14)和式(15)来求解反散射问题.把式(15)中两个等式的右端分别记为F1[f,φ1,φ2](x)+(F2′[f,φ1,φ2]fh)(x).显然,F1[f,φ1,φ2](x),F2[f,φ1,φ2](x)关于f是非线性的.给定φ1,φ2,从式(14)中求解f这个过程需要对式(15)做如下线性化处理: (16) (17) 式中:(F1[f,φ1,φ2]fh)(x),(F2′[f,φ1,φ2]fh)(x)分别表示F1[f,φ1,φ2](x),F2[f,φ1,φ2](x)在f处关于方向fh的Fréchet导数F1[f,φ1,φ2](x),(F1′[f,φ1,φ2]fh)(x),F2[f,φ1,φ2](x),(F2′[f,φ1,φ2]fh)(x)的具体形式将在本文的附录中给出. 为了进一步分析线性化方程式(16)和式(17),需要对无穷曲面函数f∈B以及更新函数fh∈B作参数化处理,这里的更新函数fh在Ω1和Ω2中的更新函数分别记为fhu和fhd.本文中我们把函数f,fhu,fhd表示成三次B-样条函数的线性组合[7-8]:设N1∈N,q,l>0, (18) (19) (20) 式中,q,l是伸缩平移常数. 这里选取的三次B-样条函数是一个分段函数,其显示表达如下: 为了方便起见,我们定义以下列向量: (21) (22) 式中:ru,rd是列向量,其元素分别为: 由于式(15)中的积分核是光滑的,所以式(15)是严重不适定的,它的线性化方程式(16)和式(17)也继承了不适定性,这就导致矩阵Ju,Jd是不可逆的.为了解决这个问题,得到式(16)和式(17)的稳定解,使用Tikhonov 正则化方法来求解式(16)和式(17),得到正则化方程为: (23) (24) 此外,还需要综合考虑散射场和透射场的测量数据对重构无穷曲面的影响,令 (25) 式中:λ是一个待定常数,λ∈(0,1),dph则为最后所求得的解.值得注意的是,正则化方程式(23)和式(24)中,矩阵Ju,Jd是复矩阵,矩阵ru,rd是复向量,为了得到一个实数解,用[ReJu;ImJu],[ReJd;ImJd],[Reru;Imru],[Rerd;Imrd]代替Ju,Jd,ru,rd. 于是可以定义重构的无穷曲面的相对误差ε(k,fr)为: 因此,当波数固定时,求解积分系统式(14)和式(15)的非线性积分方程方法的算法为: 算法1 基于单频数据重构可穿透无穷曲面的非线性积分方程方法假设对于一组波数k=(k1,k2),散射场和透射场的近场测量数据分别为ub1k(x),ub2k(x),给定相对误差ε0∈(0,1):1:选取无穷曲面的一个初始猜测f0,k,也就是在式(18)中给定一组初始系数dp,把它记为dp0;2:已知曲面fm,k(m≥0),也就是已知式(18)中的dp=dpm,k,利用Nystrm方法求解积分方程(14)可解得φm,k;3:对于得到的φm,k以及fm,k,通过解方程(23)、(24)、(25)可得到更新函数dphk,令dpm+1,k=dpm,k+dphk,然后计算对应的相对误差ε(k,fm+1,k).如果ε(k,fm+1,k)<ε0或ε(k,fm+1,k)>ε(k,fm,k),迭代停止,否则转到第2步. 对于给定的波数k和ε(k,fk),运用算法1可以得到无穷曲面的近似解fk.基于算法1,下面给出多频数据的非线性积分方程方法的迭代算法. 算法2 基于多频数据重构可穿透无穷曲面的非线性积分方程方法给定上下两个区域的单调上升的n组波数kj={(kj1,kj2)|j=1,2,…,n},对应的多频近场数据为{ub1kj(x),ub2kj(x)|j=1,2,…,n}以及相对误差ε0,初始猜测f0和下降率ρ∈(0,1):1:设k=kj,当j=1时,令f0,k1=f0,εk1=ε0,否则令f0,kj=f0,kj-1以及εkj=ρε(kj-1,fkj-1);2:运用算法1,可以得到对应于一组波数k=kj的重构曲面fkj,这时对应的相对误差为ε(kj,fkj),令j=j+1,如果j≤n,转到第1步, 否则迭代停止. 在文章的最后一部分,通过展示一些数值算例来说明非线性积分方程方法的有效性.在以下所有算例中, 设置一些参数如下: (1)入射场ui为41个点源的叠加,点源所在位置为zj=(-20+1·j,0.8),j=0,1,…,40.令式(18)、(19)、(20)中的q=0.15,l=0.05,三次样条函数基函数的个数N1=100. (4)在所有算例图片中,用实线表示真实的无穷曲面,用黑色点划线表示初始猜测的无穷曲面,用虚线表示重构的无穷曲面. 例1首先考虑一个简单的位于平面x2=0以上的可穿透无穷曲面Γf1,其表达式为 f1(t)=0.2exp(-0.4t2). (26) 在这个例子中,令无穷曲面上下区域对应的波数为k1=2,k2=6,上方区域的测量数据所占比重为λ=0.9,下方区域的测量数据所占比重为(1-λ)=0.1. 图2给出了对应0%,2%和5%噪声数据下的重构曲面. 图2 基于单频且不同噪声数据的非线性积分方程方法对无穷曲面式(26)的重构Fig.2 Reconstruction of infinite surface (26) based on nonlinear integral equation method with single frequency data and different noise data 从图2可以看到,对这种比较简单的无穷曲面,非线性积分方程方法可以获得比较精确的重构效果.针对5%噪声数据,我们想要达到比图2(c)中更加精确的重构效果,因此考虑采用多频数据,也就是多组波数的形式,这里选取的多波数为k1={2,3,4,5};k2={6,9,12,15}.使用多频数据的目的在于处理反散射问题的不适定性,以便得到更精确的重构曲面.首先给定在第一组波数下无穷曲面的初始猜测,利用非线性积分方程方法可以重构出第一组波数下的无穷曲面,并将其作为第二组波数的初始猜测,以此类推直到迭代完所有波数.以下只展示部分波数的重构结果,如图3所示. 图3 基于多频且带有5%噪声数据的非线性积分方程方法对无穷曲面式(26)的重构Fig.3 Reconstruction of infinite surface (26) based on nonlinear integral equation method with multi-frequency and 5% noise data 对比图2(c)和图3(c),很容易看到,相较于单频数据,基于多频数据的非线性积分方程方法更能达到令人满意的重构结果.有关使用单频数据与多频数据对无穷曲面重构效果的影响,我们将在例2中给出相关例子. 例2在这个例子中,我们考虑位于平面x2=0以下的可穿透的无穷曲面Γf2,其表达式为 f2(t)=-0.2exp(-0.6t2). (27) 令无穷曲面上下区域对应的波数为k1={2,3,4};k2={6,9,12},上方区域的测量数据所占比重为λ=0.65,下方区域的测量数据所占比重为(1-λ)=0.35.先考虑采用单频数据,利用一组对应的波数重构一个曲面,对比不同波数的重构效果.然后考虑采用多频数据,令第一组波数重构的无穷曲面作为第二组波数的初始猜测,以此类推直到迭代完所有给定的波数.这里只展示部分波数的重构结果,图4(a)~(c)给出了无噪声情形下单频数据的重构曲面,图4(d)~(f)给出了无噪声情形下多频数据的重构曲面. 图4 基于不同频率且无噪声数据的非线性积分方程方法对无穷曲面式(27)的重构Fig.4 Reconstruction of infinite surface (27) based on nonlinear integral equation method with different frequency and noise-free data 从图4(a)~(c)可以看出,如果仅采用单频数据对无穷曲面进行反演,效果并不理想,尝试换一组更大的波数,但是仍然没有奏效,如果继续加大波数,反而使得重构效果更加糟糕,不能得到令人满意的重构效果.相比之下,如图4(d)~(f)所示,采用多频数据重构的效果比单频数据更好,重构的无穷曲面更为准确.因此,如果需要重构更为复杂的无穷曲面,首先应该考虑使用多频数据. 在使用多频数据能获得比较精确的重构效果的前提下,我们考虑带有噪声的数据的重构效果.图5(a)~(f)分别给出了带有2%、5%噪声的多频数据的数值重构曲面. 图5 基于多频且带有不同噪声数据的非线性积分方程方法对无穷曲面式(27)的重构Fig.5 Reconstruction of infinite surface 式(27) based on nonlinear integral equation method with multi-frequency and different noise data 从图5(a)~(f)可以看出,即使是噪声数据,在多频的情况下,利用非线性积分方程方法,仍然能得到比较精确的重构效果. 例3在这个例子中,考虑一个较为复杂的可穿透无穷曲面Γf3,该曲面含有多个局部扰动,其表达式为 (28) 令无穷曲面上下区域对应的波数为k1={2,3,4,5,6,7,8,9};k2={6,9,12,15,18,21,24,27},上方区域的测量数据所占比重为λ=0.65,下方区域的测量数据所占比重为(1-λ)=0.35.这里只展示部分波数的重构结果,图6 给出了基于多频且无噪声数据的非线性积分方程方法对无穷曲面Γf3的重构. 图6 基于多频且无噪声数据的非线性积分方程方法对无穷曲面式(28)的重构Fig.6 Reconstruction of infinite surface (28) based on nonlinear integral equation method with multi-frequency and noise-free data 从图6中可以看出,对于较为复杂的无穷曲面,在多频的情况下,利用非线性积分方程方法,仍然能得到比较精确的重构效果. 例4在这个例子中,将探讨无穷曲面上下区域的测量数据所占比重对重构无穷曲面的影响.考虑一个可穿透的无穷曲面Γf4,该无穷曲面的一部分位于平面x2=0以上,一部分位于平面x2=0以下,其表达式为 f4(t)=0.3exp(-1.3(t-1)2)-0.4exp(-1.8(t+2)2). (29) 令无穷曲面上下区域对应的波数为k1={2,3,4,5,6};k2={6,9,12,15,18},上下方区域的测量数据所占比重作为控制变量,其他参数不变.这里只展示部分波数的重构结果,图7(a)~(l)分别给出了上下方区域占不同权重的情形下对可穿透无穷曲面Γf4利用无噪声多频数据进行重构的曲面. 从图7中(a)~(l)的重构效果可以看出,当控制其他参数不变的情况下,改变上下方区域的测量数据所占的比重会对无穷曲面的重构产生很大的影响.如图7(a)~(c)、图7(d)~(c)所示,如果只采用上方测量数据或者只采用下方测量数据,很显然并不能达到令人满意的重构效果; 图7 基于不同权重的多频且无噪声数据的非线性积分方程方法对无穷曲面式(29)的重构Fig.7 Reconstruction of infinite surface (29) by nonlinear integral equation method based on multi-frequency and noise-free data with different weights 例5在这个例子中,考虑一个全局扰动的可穿透无穷曲面Γf5,其表达式为 f5(t)=0.2sin(πt)+0.1cos(πt). (30) 令无穷曲面上下区域对应的波数为k1={2,4,6,8,10};k2={6,12,18,24,30},上方区域的测量数据所占比重为λ=0.85,下方区域的测量数据所占比重为(1-λ)=0.15.在这个例子中,对点源做出一些改变,增加了点源的个数,点源所在位置为zj=(-30+0.75j,0.6),j=0,1,…,80.这里只展示部分波数的重构结果,图8给出了基于多频且无噪声数据的非线性积分方程方法对无穷曲面Γf5的重构. 图8 基于多频且无噪声数据的非线性积分方程方法对无穷曲面式(30)的重构Fig.8 Reconstruction of infinite surface (30) based on nonlinear integral equation method with multi-frequency and noise-free data 从图8中可以看出,对于全局扰动的无穷曲面,在多频的情况下利用非线性积分方程方法,可以得到比较精确的重构效果,但是一些细节处的重构效果次于局部扰动的重构效果. 通过本节中的例子,可以看到非线性积分方程方法可以很好地解决可穿透无穷曲面的反散射问题.相较于单频数据的非线性积分方程方法,多频数据的非线性积分方程方法能够给出更令人满意的重构效果,即使是噪声数据,在多频的情况下仍然能得到比较精确的重构效果.通过比较近似局部扰动与全局扰动的情形,可以看到非线性积分方程方法对近似局部扰动的无穷曲面的重构效果更好一些.同时,可发现上下方区域测量数据的比重也会对无穷曲面的重构产生影响,在重构的过程中选取恰当的比重就显得非常重要.


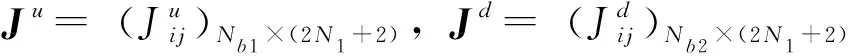






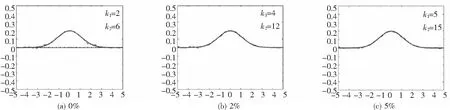


如果令上下两方测量数据的占比一样,如图7(g)~(i)所示,能有较好的重构效果;
如果令上方的测量数据所占比重稍大于下方数据,如图7(j)~(l)所示,发现其重构效果比图7(g)~(i)更加精确.