林奕武, 林培年, 程健燊
(广东金融学院 金融数学与统计学院,广东 广州 510521)
近几十年来,抛物型方程和抛物型方程组解的爆破问题一直备受关注,很多学者开始进行这方面研究并发表了相关论文.Tao等[1]考虑了有界凸区域Ω∈RN(N≥1)内系数随时间变化的反应扩散系统
的爆破现象,采用 Kaplan方法、子解和超解方式并结合改进的微分不等式技术,求出了爆破时刻的上下界.Ding等[2]对有界凸区Ω∈RN(N≥2)内的反应扩散方程
在Dirichlet边界条件下的爆破现象进行研究.Tang[3]研究有界凸区域Ω∈RN(N≥1)内一类具有梯度非线性的反应扩散系统
的爆破问题.通过构造适当的辅助函数,并利用Payne-Weinberger和Scott方法,得到爆破时间下界.Ding等[4]主要讨论有界凸区Ω∈RN(N≥2)内一类拟线性反应扩散问题
解的爆破现象.采用微分不等式技术并结合极大值原理,求出了爆破时间上下界.Ding等[5]主要讨论了有界凸区Ω∈RN(N≥2)内非线性反应扩散方程
在非局部边界条件下的爆破现象.Shen等[6]对多孔介质方程组
在有界凸区Ω∈RN(N≥2)解的爆破现象进行探究.运用Sobolev不等式并结合微分不等式方法对其求解得到爆破时间上界.Liu[7]对Robin边界条件下非线性非局部多孔介质方程
在有界凸区域Ω∈R3上的爆破问题进行研究.利用Hölder不等式确定爆破发生时爆破时间的下界,并给出爆破不发生的条件.Liu等[8]在有界凸区Ω∈R3内分别对Dirichlet边界条件和齐次Neumann边界条件下的非线性非局部多孔介质方程
的爆破问题进行探究.Payne等[9]对有界凸区Ω∈R3上的半线性问题
进行探讨.在构造辅助函数的基础上,结合微分不等式方法推导求出爆破时刻,同时基于比较原理提出了第2种方法.Payne等[10]将文献[9]的成果推行到更普遍的抛物方程
ut=div(ρ(u)gradu)+f(u).
Payne等[11]对一类半线性热方程在Neumann边界条件下的初边值问题进行探讨.克服了文献[9]中齐次边界条件为Dirichlet时Sobolev不等式的不足,推导得到爆破时间的一个下界和一个上界.Payne等[12]对有界凸区Ω∈RN(N≥2)内半线性和非线性问题
的爆破现象进行探究.确定了爆破发生时间的下界,而且给出了爆破准则以及不产生爆破的一些限制主体.Payne等[13]对有界凸区域Ω∈RN(N≥2)内一类半线性热方程
在非线性边界条件下的爆破现象进行探讨.Payne等[14]对有界凸区Ω∈RN(N≥2)中的初始边界问题
进行研讨.Liu等[15]对一类具有梯度非线性的抛物方程
在非线性边界的爆破现象进行研讨.李远飞[16]考虑在有界凸区域Ω∈R3的一个更加初边值问题
求出了爆破产生时的下界.李远飞等[17]在Neumann边界条件下对非线性抛物方程
的初边值问题进行研讨.在恰当假设基础之下,得到了爆破发生时的爆破时间下界以及爆破不发生的前提条件.Chen等[18]对有界凸区Ω∈RN(N≥2)中一类非线性抛物问题
的爆破现象进行探讨.运用微分不等式的方法求出爆破时刻的下界.Payne等[19]研究趋化模型
在Ω∈R3的爆破问题.求出爆破时间下界,并明确了保证不产生爆破的准则.Payne等[20]推导得到更一般的抛物型方程组在爆破产生时的爆破时间下界.Li等[21]探讨有界凸区域Ω∈RN(N=2,3)内完全抛物型Keller-Segel方程组
在Neumann边界条件下的初边值问题.推导求出有限时间的爆破以及全局时间无界解.李远飞[22]对Robin边界条件下有界凸区域Ω∈RN(N≥3)内Keller-Segel抛物体系解的爆破问题进行了研究,并获得类似结果.
本文中,笔者对如下非线性Keller-Segel趋化模型进行探讨:

(1)
(2)

(3)
u=u0(x),v=v0(x),在Ω·t=0上.
(4)
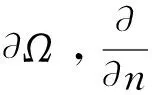
为了方便起见,假设
D(u)=us+1,S(u)=urs,r>0.
(5)
目前,对Keller-Segel趋化模型解的爆破现象的研究,人们更为关注简化的抛物线模型和椭圆模型.由于扩散和迁移2种机理的存在,具有非线性扩散项的Keller-Segel模型表现出复杂的动力学行为,处理难度加大.本文中,笔者主要讨论具有扩散项的高维空间抛物体系解的爆破问题.
采用构造适当的辅助函数,然后基于微分不等式方法并结合 Sobolev的嵌入定理,得出了在高维空间RN(N≥3)中方程(1)~(4)解的爆破时间下界.
引理1[18]对于任意正常数x1,x2,若0<α<1,有如下Hölder不等式:
为了得到所需结论,定义辅助函数φ=φ(t)如下:

(6)
定理1假定u=u(x,t)和v=v(x,t)是方程组(1)~(4)在有界星型区域Ω∈RN(N≥3)上的经典非负解.那么在(6)中所定义的辅助函数φ(t)必满足如下微分不等式
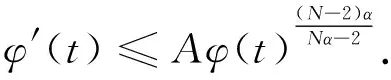
(7)
由(7)可得到爆破时间t*具有如下下界
(8)
其中A与α均是后面定义的正常数,并且α满足α<1.
定理1的证明将分为以下几个引理来完成.
引理2(6)中定义的辅助函数φ(t)具有如下性质

(9)
其中ε1是后面定义的正常数.
证利用(1)~(5)以及散度定理,可得
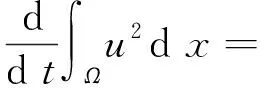
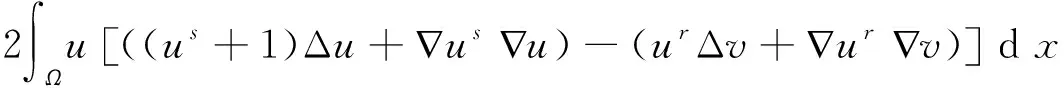


(10)




(11)
其中ε1是后面定义的正常数.
结合(10)和(11),可以得到

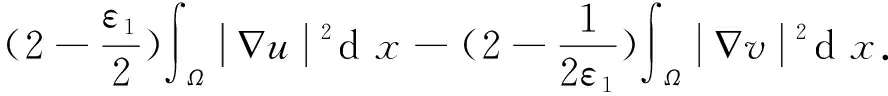
使用等式
|∇un|2(q+1)=|nun-1∇u|2(q+1),
可以得到

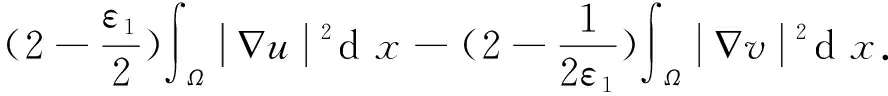
引理2得证.



(12)

证使用Hölder 不等式,得


(13)
选择x1,x2和α使得

则有
利用引理1的结果,可得到

(14)
对于N≥3,具有如下Sobolev嵌入关系
因此,得到
(15)
其中c1是嵌入常数.
将(14)和(15)进行组合,得
利用Young不等式,可以得到


(16)
其中ε2是后面定义的正常数.
结合(13)和(16),可以得到


引理3得证.
引理4对于能量表达式φ(t),有如下性质

(17)
证结合引理2与引理3,得到


(18)

(19)
(20)
选择ε1使得




(21)
同理,选择足够小的ε2,使得


同时,可以得到
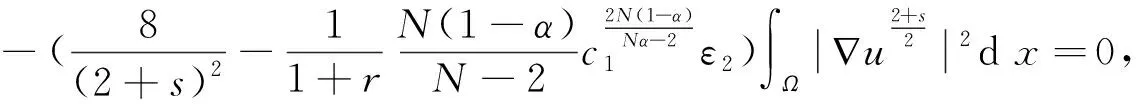
结合(18)~(21),可以得到

引理4得证.
引理5能量表达式φ(t)满足如下不等式
(22)
同时,爆破时间t*有如下下界
(23)
证由(17),可以得到

(24)
在(24)中使用不等式
am+bm≤(a+b)m,a,b>0,m>1,
得到
(25)
其中常数A定义为

(25)可以改写为
(26)
不等式(26)从0到t的积分,得到
(27)
取极限为t→t*,得到
(28)
定理证明完毕.
本文中,笔者研究了高维空间RN(N≥3)上一类Keller-Segel趋化模型在齐次Neumann边界条件下解的爆破问题.利用能量方法,运用微分不等式技巧以及高维Soblev嵌入不等式,得到解的爆破时间下界.由于以往研究Keller-Segel趋化模型的爆破时间主要是估计爆破时间上界,因而解的下界估计更为困难.关于该模型解的爆破时间下界的研究大多是在低维空间,目前还未发现具有非线性扩散项的Keller-Segel趋化模型解在高维空间RN(N≥3)上的爆破问题的研究,将以往的结果由低维空间推广到了高维空间.后续的研究工作将进一步推广到Dirichlet边界条件下,非线性边界条件下以及具有变系数的Keller-Segel趋化模型解的爆破问题研究.由于非线性边界条件的复杂性以及在变系数的抛物系统对参数设置的要求更加精妙,此类问题的研究将更具复杂性和难度.
猜你喜欢维空间趋化下界三维趋化流体耦合系统整体解的最优衰减估计数学年刊A辑(中文版)(2022年1期)2022-08-20一个不等式的下界探究中学数学研究(江西)(2022年8期)2022-08-09方程的两个根的和差积商的上下界数学大世界(2021年10期)2021-06-05Update on Fengyun Meteorological Satellite Program and Development*空间科学学报(2020年5期)2020-04-16三七根系分泌物中几种成分对根腐病原菌生长的影响南方农业学报(2020年12期)2020-03-24Lower bound estimation of the maximum allowable initial error and its numerical calculationAtmospheric and Oceanic Science Letters(2018年5期)2018-12-07恶臭假单胞菌UW4中趋化受体蛋白的克隆、表达及鉴定天津农业科学(2018年5期)2018-06-23假单胞菌趋化性研究概述天津农业科学(2017年8期)2017-08-11对一个代数式上下界的改进研究数学学习与研究(2016年18期)2017-01-07从零维到十维的空间之旅大众科学(2016年11期)2016-11-30


